Using Complicated Mathematical Model in the Control Loop For the Technological Process Control System
Sharikov F.I.1*
Sharikov I.V.2
1Researcher of Department of Automation of Technological Processes and Industrial Plants, Saint Petersburg Mining University, Saint Petersburg, Russia |
AbstractOptimal control for technological process with distributed state variables and with a large dead times in the object is discussed. Very important problem for creating control system with using the object model in the control loop are considered. It has been shown that heat flux calorimetry is an effective experimental technique for the development of an exothermic (or endothermic) chemical process model based upon the process kinetic model and hydrodynamic media inside object. Successful application of this approach for the creation of mathematical models and their further use in the corresponding control systems has been demonstrated for two different important industrial processes – sintering process in the preparation of cement clinker in the tubular rotating kiln and modification process of epoxy resins with butanediol-1,4 for further synthesis of epoxy-urethane polymers with improved physical and mechanical properties. The mathematical model of a technological object makes it possible to specify the optimal operating mode for each of the considered processes and implement the optimal control conditions. |
Licensed: |
|
Keywords: |
|
| (* Corresponding Author) |
Funding: This study received no specific financial support. |
Competing Interests:The authors declare that they have no competing interests. |
1. Introduction
Closed control systems based upon monitoring deviation with a feedback loop are widely used in industry for various technological objects [1, 2]. However, they cannot be successfully used for controlling objects with distributed state variables and with a large dead time – e.g., large tubular and batch reactors, shell tubular heat exchangers, distillation columns and so on – in case of supporting a control variable at the output of the apparatus [3]. Besides, a control system via deviation usually can not be used in case of a potentially dangerous object, as deviation of regulation parameters from the given values in this case is not permitted from the viewpoint of the process safety [4, 5].
1.1. Formulation of the Optimal Control Task
In case of an object with distributed parameters one should use a predicative control system which is able to generate control actions in order to provide the corresponding compensating actions for input disturbances while the process is run through a regulating channel. Generation of such control signals is based upon analysis of the object input variables and an exact algorithm of input variables transformation into output variables. In this case it is possible to use calculation methods that take into account transfer functions of passing a disturbance through regulation channel [2, 4]. In these cases a control system may generate the necessary control actions that should support regulated values at the given level. If we use a computer in the control loop it is possible to use a mathematical model of the object for predicting the object behavior in case of input disturbances. In this case the control system may be called the “control system with a fast model” in the control loop. Due to this solution a mathematical model of the object makes it possible to obtain an object response faster than the real object response, and it is possible to analyze it and to generate an optimal control action in order to compensate any possible deviations of regulated variables from the set points.
A principle scheme of the control system with a “fast model” in its control loop is given in Figure 1.
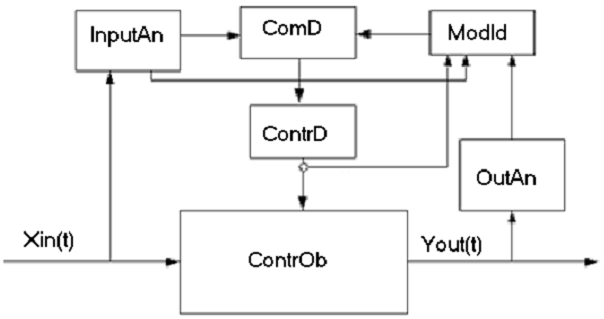
Figure-1. Scheme of disturbances control with applying a “fast model” in the control loop.
ContrOb – an object to be controlled; ContrD – a control device; InputAn – input analyzer; OutAn – output analyzer; ModId – model identifier; ComD - computing device; Xin(t) - vector-function of input variables; Yout(t) - vector-function of output variables.
Input variables are passed through the device InputAn –input analyzer. After that the vector of input parameters and the vector of input disturbances both proceed to a computing device ComD and also to ModId – model identifier. The information about current values of the control vector parameters comes to ModId as well. An inverse task is solved in ModId and current parameters of the mathematical model are specified in the result. The time delay value should be taken into account for every signal. It is a very important step of the whole identification procedure. The real time delay values may be either specified or measured directly in special experiments. In this case the typical preset disturbances are acted on the object. Analyzing the result of these disturbances one can specify the exact values delay time value for every control channel.
After its identification the model is transferred to a computer device where the optimal control action values are calculated. These optimal control action values correspond to the current state of a controlled object. At present such control schemes are used to control some complicated processes characterized by variegated disturbances of input variables. On the base of available experience to control the systems of such kind it is possible to specify the critical deviation state variables that should be identified through the mathematical model. This procedure allows to fulfill the identification procedure not very often and to raise the processing speed of the control system.
1.2. Creating Models for Control Systems
At creating models for control systems it is very important to predict the object performance in a wide interval of changing the variables. The models based upon chemicals kinetics and hydrodynamics equations of an object are very perspective in this case. A number of well-known simplified hydrodynamic models are commonly used, such as an ideal mixing model, a plug flow model and some combinations of these models. As for kinetic models – the models based upon heat flux calorimetry data are very promising. The use of calorimetry for kinetic study and modelling is based upon the fact that overall heat generation rate is connected with the chemical reaction rates as follows:
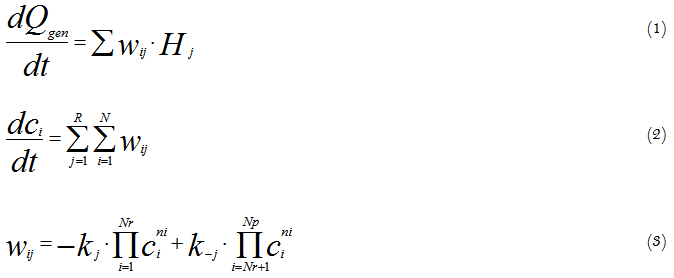
Where:

The procedure that is usually used for kinetic parameters determination from the experimental data is based upon searching the kinetic parameters to agree the condition of a minimal mismatch between the experimental data and the process modelling results. The sum of deviation squares between experimental data and modelling results is usually used as a measure of such mismatch in accordance with the Equation 4:
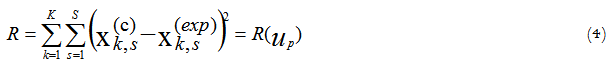
Where:
k - index of a time point on a kinetics curve;
s - index of a measured state variable in a kinetics experiment;
c - calculated data;
exp - experimental data;
K - number of experimental points of a kinetics curve;
S - number of the measured state variables of a mathematical model;
up – the required kinetics parameters (pre-exponential factors, activation energies, reaction orders, heat effect of reaction).
Various nonlinear programming methods are used at searching the extremum. Calculated data values and state variables are generated through numerical solution of the mathematical model differential equations with applying the Runge-Kutta method or LSODA method [6, 7].
2. Results and Discussion
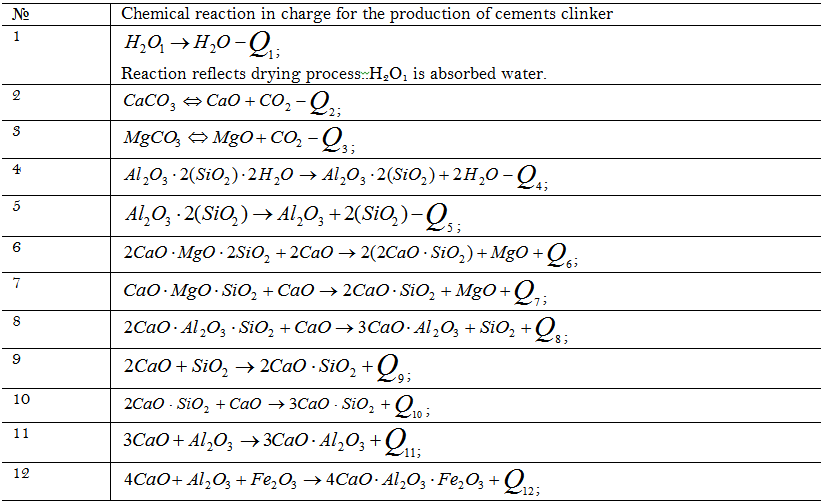
The process of cement clinker production in a tubular rotary kiln is the first one to illustrate the approach being developed. Experimental study was carried out with applying NETSCH STA 449 thermal analyzer. Sample mass loss and heat generation (absorption) rate were experimental responses. Chemical reactions that take place in a tubular kiln at sintering cement clinker were used in the corresponding kinetic model [6, 8] see Table 1.
Kinetic parameters have been found at solving the inverse kinetic task in accordance with the Equation 4 in ReactOp program package [7, 9]. Heat effect values, activation energy and pre-exponential factor value logarithms of the rate constants are presented in Table 2.
| Table-2. The found kinetic parameter values for the kinetic model of cement clinker production. |
| Mineral of charge | Kinetic parameter values | |
1 |
CaCO3 | |
| ln(Ko)/min-1 | 13.37 |
|
| Ea/kJ×mol-1 | 102.17 |
|
| ln(Keo)/min-1 | 15.01 |
|
| Ee/kJ×mol-1 | 60.0 |
|
2 |
MgCO3 | |
| ln(Ko)/min-1 | 2.61 |
|
| Ea/kJ×mol-1 | 89.63 |
|
| ln(Keo)/min-1 | 93.18 |
|
| Ee/kJ×mol-1 | 187.06 |
|
| (-H)/kJ×kmol-1 | -68819,37 |
|
3 |
Al2O3(SiO2)2(H2O)2 | |
| ln(Ko)/min-1 | 4.9 |
|
| Ea/kJ×mol-1 | 48.35 |
|
| (-H)/kJ×kmol-1 | -237744 |
|
4 |
NaAlO2(SiO2)6(H2O)2 | |
| ln(Ko)/min-1 | 9.86 |
|
| Ea/kJ×mol-1 | 20.84 |
|
| (-H)/kJ×kmol-1 | -66948 |
|
5 |
Al2O3(H2O)3 | |
| ln(Ko)/min-1 | 10.47 |
|
| Ea/kJ×mol-1 | 11.22 |
|
| (-H)/kJ×kmol-1 | -52891 |
|
6 |
NaAlO2(SiO2)6(H2O)2 | |
| ln(Ko)/min-1 | 2.19 |
|
| Ea/kJ×mol-1 | 48.84 |
|
| (-H)/kJ×kmol-1 | -102920 |
|
7 |
Fe(OH)3 | |
| ln(Ko)/min-1 | 4.73 |
|
| Ea/kJ×mol-1 | 36.16 |
|
| (-H)/kJ×kmol-1 | 10292 |
|
8 |
Al2O3(SiO2)2 | |
| ln(Ko)/min-1 | 20,32 |
|
| Ea/kJ×mol-1 | 150,3 |
|
| (-H)/kJ/×kmol-1 | -66948 |
|
9 |
(CaO)2MgO(SiO2)2 | |
| ln(Ko)/min-1 | 13,2 |
|
| Ea/kJ×mol-1 | 150,1 |
|
| ln(Keo)/min-1 | 103823 |
|
10 |
(CaO)2Al2O3SiO2 | |
| ln(Ko)/min-1 | 23,21 |
|
| Ea/kJ×mol-1 | 250,34 |
|
| (-H)/kJ×kmol-1 | 10292 |
|
Comparison of experimental data and modeling results is presented in Figure 2 (a,b). The modelling results have been calculated with applying the found kinetic parameters values see Table 2.
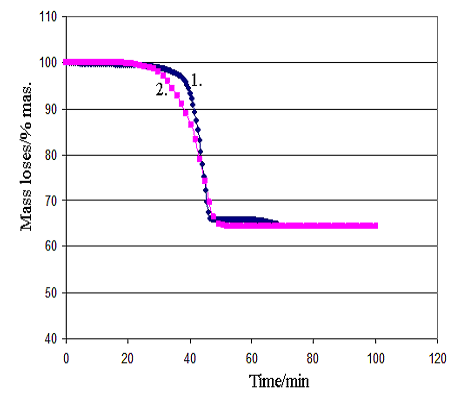
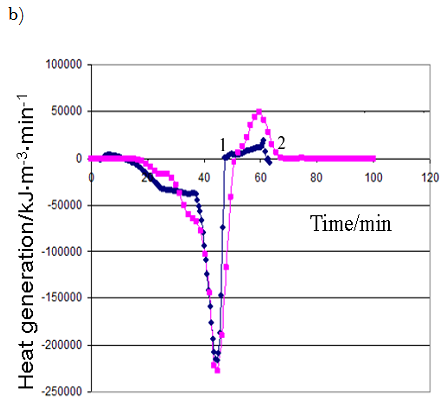
It can be concluded see Figure 2 that the experimental data are satisfactorily described with the kinetic model and it may be used for further modeling of cement clinker production under industrial conditions.
The mathematical model of sintering process of the cement charge in a rotary tubular kiln has been developed [4] on the base of this approach. The model represents a system of differential equations describing change of the component concentrations in gas and in solid phases along the length of a tubular kiln.
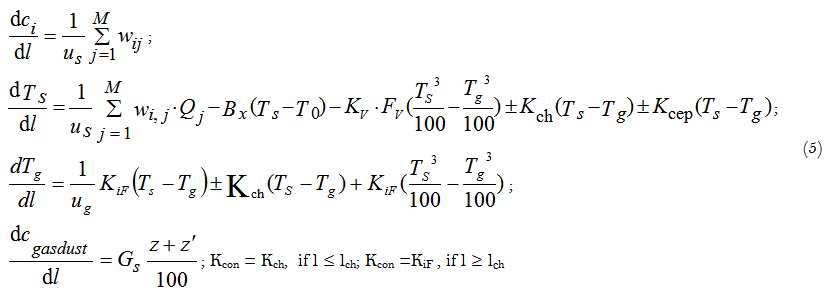
Where:
l/m – current kiln length; L/m – total kiln length;
c/kmol∙m-3 – concentration of the i-th component in reaction mixture;
us/m∙s-1 – linear velocity of a solid material movement;
wi,j/kmol∙m-3∙s-1 – rate of the i-th component concentration change in the j-th reaction;
Tg and Ts/K –temperatures of gas and solid phase, respectively;
z’/% – dust fraction circulating in the kiln;
z/% – dust fraction removed from the kiln;
T0/K - temperature inside the kiln; Bx/m-1 – heat exchange parameter;
Kch/W∙m-2∙K – heat transfer coefficient in the chain curtain zone of the kiln;
lch/m - chain curtain zone length;
M - number of chemical reactions, Qj/kJ/kmol-1 – heat effect of the j-th reaction; KiF/W∙m-2∙K-1 – heat transfer coefficient in the zone free from chain curtain; cngasdust/kg∙m-3 – dust concentration in the gas phase;
Gs/kg×kg-1 - dust mass fraction inside the kiln;
Kcon/m-1 – parameter of convective heat exchange;
FV/m2×m-3 – specific radiation surface.
Due to a counter-current movement of gas and solid phases in the kiln the mathematical modelling represents a boundary problem with the boundary conditions, given at both ends of the integration interval. The method of successive iterations has been used for solving this problem.
2.1. Modelling the Process of Epoxy Resin Modification with Butanediol-1,4.
Modification of epoxy resins with butanediol-1,4 alcohol is another chemical process that has been discussed and verified with the proposed approach. Modification is a powerful instrument for expanding the functionality and improving physical and mechanical characteristics of final polymers or polymer coatings [10, 11]. Kinetic study of modification reactions of chlorine containing epoxy resins was done with the use of heat flux calorimetry. C80 Calvet calorimeter (SETARAM Instrumentation) was applied. Heat generation rate curves were taken as experimental responses together with the analysis result data in final points. The following kinetic scheme has been proposed for the modification process [12]:
1) NaOH + HO-R-OH ↔ Na+ + HO-R-O- + H2O
2) {EPO} + HO-R-O- → {MODIF}-O-
3) {MODIF}-O- + HO-R-OH → {MODIF}-OH + HO-R-O- (6)
4) V(BD) → HO-R-OH + NaOH (HO-R-O-)
5) {EPO} + HO-R-OH → {MODIF}-OH
The process mathematical model has been developed on base of kinetic study in the form of the following system of differential equations:
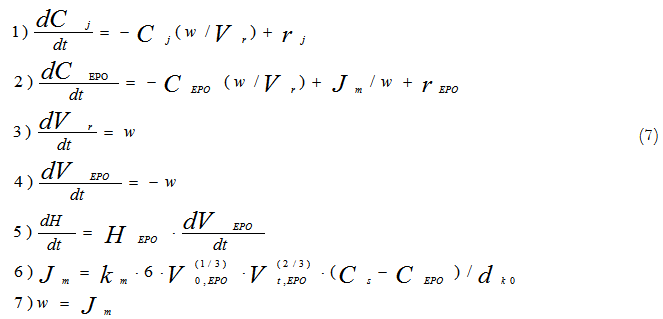
Where:
Ci /kmol×m-3 – concentrations of all components of the reaction mixture except for concentration epoxy groups;
СEPO/kmol×m-3 – epoxy groups concentration in the reaction phase;
Vr/m3 – volume of reaction phase;
VEPO/m3 – volume of epoxy resin in the reactor;
Jm/kmol×m-3 – mole flow of epoxy groups in the reaction phase;
v/m3×s-1 – volume flow in the reaction phase;
ddr,0/m – drop volume of dissolving phase at initial time moment;
dEPO/kmol×m-3 – mole density of an epoxy group.
All generated heat is distributed uniformly between the phases and heat exchange is not taken into account. ReactOp Cascade 3.20 program package was used for solving the inverse kinetic task [7, 9]. Comparison of experimental data and modelling results is presented in Figure 3a, b
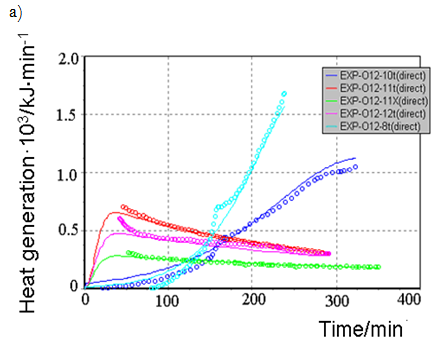
Figure-3a. Comparison of experimental data and modeling results at various initial conditions: |
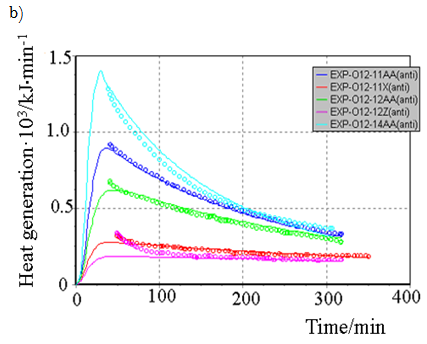
Figure-3b. Comparison of experimental data and modeling results at various initial conditions: |
The problem of searching an optimal temperature profile in the reactor has been formulated and solved on the base of the developed mathematical models.
For production cement clinker in tubular rotary kiln we consider temperature change profile along the kiln length as the running control parameter:
In this case, the optimization criterion is the functional value expressed by the value of tricalcium silicate concentration at the exit of the kiln:
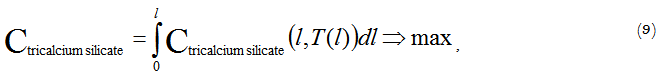
In this form the optimization task is a variational calculus problem, as the control function of T (l) is the control variable. If we represent the desired optimum temperature profile as a piecewise linear approximation of the control function along the length, we can proceed from the variational problem to the ordinary problem of finding an extremum of the several variables function:
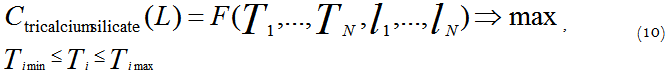
where L – full length of the kiln.
In this case the controls (certain points and the temperature values in these certain points) will be found in an allowable control region. The restrictions may be set separately for every section of the temperature profile. This is a typical problem of an extremum with inequality constraints. To solve such a problem the method of nonlinear programming implemented in the program package ReactOp Cascade 3.20 may be used [7, 9].
We have used a simplified mathematical model with the equations that describe chemical reactions in the solid phase and oxygen concentration in the solid phase. The equations of heat transfer between the phases and the equation for the temperature of the solid and the gas phase cannot be used, because the solid phase temperature is a control variable that we have to find at solving the optimization problem. Graphs of the main component concentrations found for the proposed optimal temperature profile are given below.
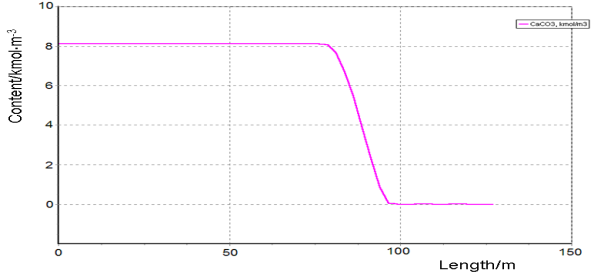
Figure-4. Calcium carbonate content loss as a function of the kiln length at firing the raw mixture in the production of cement clinker. |
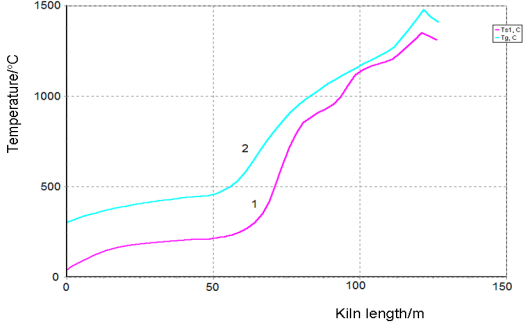
Figure-5. Temperature profile of Solid (1) and Gas (2) phases inside the kiln under optimal technological conditions. |
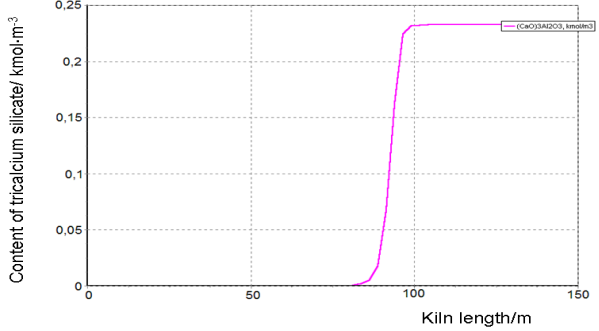
Figure-6. Generation of tricalcium silicate (an objective) along the kiln length during firing the raw mix for the process of cement clinker production under optimal conditions. |
It has been found that the objective value under optimal conditions is 12% greater compared to the commonly used operating conditions.
The results obtained prove the effectiveness of applying mathematical modelling for the task of determining the optimum process conditions in tubular rotary kilns at calcination processes. To develop a mathematical model of a definite kiln with the known chemical composition of raw material it is necessary to study the kinetics of chemical reactions using, e.g., TG-DSC technique. The proposed algorithm of searching an optimal temperature profile has been used in the control system of a cement clinker production plant in Russian Federation. Technological scheme and the control loop of this process are presented in Figure 7.
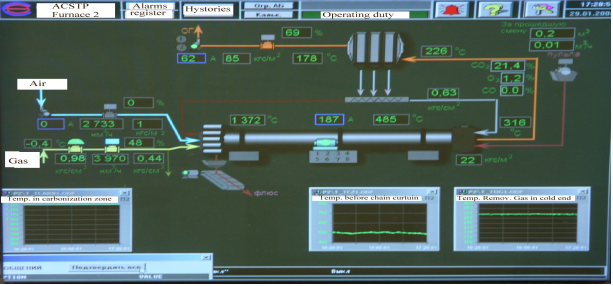
Figure-7. Technological scheme and the corresponding control system for the process of cement clinker production. |
Calculated temperature profile has been used to fix the temperature set points for control system along the kiln length. The flows of Gas (methane) and Air have been used as control actions.
The following strategy of optimal control has been proposed in the result. First, one should set up the kiln productivity for the final product and then select the necessary composition of the charge. Then XRD quantitative phase analysis of the charge composition is done in order to verify its mineralogical composition and write the corresponding chemical reactions. A kinetic study of the charge sample firing is done using TG/DSC technique. Kinetic parameters of the process mathematical model are searched on the base of experimental data in accordance with the procedure described above and an optimal temperature profile is generated. Material and heat balance of the process is estimated via solving a direct kinetic task with the developed process model for the optimal temperature profile.
Consumption of natural gas and air is selected for the optimal temperature profile with applying the process mathematical model.
2.2. Optimization of the Epoxy Resin Modification Process
An optimal temperature profile for the chosen chemical reactor should provide the maximal concentration of the final product (modified epoxy groups) at the end of the process. Temperature of heat exchange facilities (temperatures of cooling water and heating steam) were chosen as control actions. These control actions should provide implementation of the optimal temperature profile with taking into account the disturbances. The values of optimal control actions in the control loop, calculated with the mathematical model in block ComD see Figure 1 are given in Figure 8. These control actions are transferred to the controller unit. The proposed control scheme is given in Figure 9.
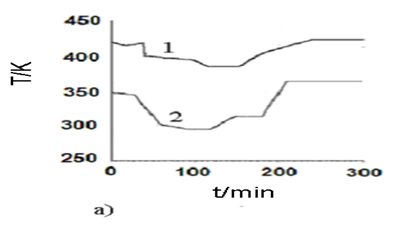
Figure-8а . Optimal control actions for the process of epoxy resin modification in the chosen stirred batch reactor as a function of time. |
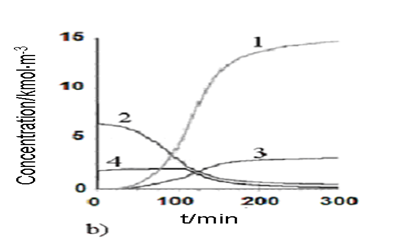
Figure-8b. Simulated heat generation and component concentration values under the process optimal control actions as a function of time. |
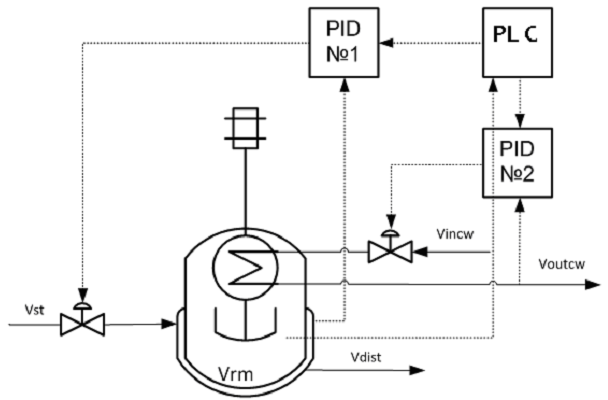
Figure-9 . Optimal control scheme for the process of epoxy resins modification with butanediol-1,4 in a stirred batch reactor. |
Vrm – modification reactor; Vst – input of heating steam in the jacket; Vdist – output of distillate from the jacket; Vincw – input of cooling water into the coil; Voutcw – output of cooling water from the coil; PID №1 – temperature regulator in the steam jacket; PID №2 – temperature regulator in the cooling coil; PLС – programmed logic controller.
3. Conclusion
- Analysis of the control problem for a complicated technological process with a considerable heat generation/consumption has been carried out.
- Experimental technique based upon TG/DSC or heat flux calorimetry and kinetic modelling has been proposed to develop a detailed mathematical model with high predictive ability for a real technological process.
- Optimal process conditions for two discussed technological processes have been established with the developed mathematical models that include chemical reaction mechanism of the process, reactor hydrodynamics, heat and mass transfer phenomena.
- The proposed approach has been applied for solving the optimal control task for two real industrial processes with taking into account the acting disturbances – on the base of the detailed mathematical models developed through kinetic modelling.
References
[1] K. P. Vlasov, "Automatic control theory," ed Tutorial, Kharkov: Humanitarian Centre, 2006, p. 531.
[2] Е. S. Benkovich, U. B. Kolesov, and U. B. Senichenkov, "Practical modeling of dynamics systems. SPb: BChV-Petersburg," p. 464, 2002.
[3] I. V. Miroshnik, "Automatic control theory. Nonlinear and optimal systems," ed Tutorial, SPb: Piter, 2006, p. 272.
[4] C. H. Jay and U. M. Andrew, "Modern control principles and applications," ed New York: McGraw-Hill Book Company, 1972, p. 544.
[5] B. Alberto, M. N. Manfred, and R. Lawrence, "Model predictive control," ed: MathWorks, 2010, p. 205.
[6] Y. Sharikov, F. Sharikov, and O. Titov, "Mathematical modeling of processes in the tubular rotary kiln. LAP, Germany," p. 104, 2013.
[7] Y. V. Sharikov and I. N. Beloglazov, "Modeling of systems. Part 2," ed Edition of Saint-Petersburg Mining University: Saint-Petersburg, 2012, p. 118.
[8] Y. V. Sharikov, F. Y. Sharikov, and O. V. Titov, "Optimization of process conditions in a tubular rotary kiln with applying TG/DSC technique and mathematical modeling," Journal of Thermal Analysis and Calorimetry, vol. 122, pp. 1029-1040, 2015.
[9] Y. V. Sharikov and I. N. Beloglazov, "Modeling of systems," ed Part 1. Edition of Saint-Petersburg Mining University: Saint-Petersburg, 2011, p. 108.
[10] D. C. Webster and A. L. Crain, "In: A.O. Patil, D.N. Schulz, B.M. Novak (Eds.)," Functional polymers: Modern synthetic methods and novel structures. Am. Chem. Soc, vol. 704, pp. 303-320, 1998.
[11] C. W. Dean, "Cyclic carbonate functional polymers and their applications," Progress in Organic Coatings, vol. 47, pp. 77-86, 2003.
[12] F. I. Sharikov and I. V. Sharikov, "Kinetic study of modification of chlorine containing epoxy resins with using heat flux calorimetry," International Research Journal, vol. 5, pp. 129-132, 2014.