Non-Linear Economies of Scale in Food Production: The Case of Norwegian Bakeries 

 

Leiv Opstad^1*
Robin Valenta²

1,2NTNU Business School, Trondheim, Norway.	Abstract The bakery industry has a rich history.  Its modern forms involve both manufacturing products and delivering them to customers.  Both small bakers and large producers sell their products to the supermarket.  The largest bakeries export a wide variety of baked foods. The sector is a large employer and it has been thoroughly studied internationally. However, only a small number of studies have analysed the baked goods sector, often due to the lack of categorization of bakeries in the data. In this article, we use public statistics on Norwegian bakeries to study their economies of scale. The profitability of large bakeries persistently exceeds the average rate. New bakeries are equally likely to succeed or fail in the long run.  Many new bakeries enter the market as a result of tough competition and a long period of high sector probability but it is difficult for them to survive. Those that must leave the market are mostly new entrants. Despite their difficulties, small and medium-sized bakeries are more profitable than new start-up businesses. We investigate the non-linear relationship between size and profitability as well as between and within bakeries.
Licensed: This work is licensed under a Creative Commons Attribution 4.0 License.
Keywords: Bakery GMM estimators Non-linear f scale effects Profit persistence Survival. JEL Classification D01; D21; D24.
Received: 15 August 2022 Revised:  3 October 2022 Accepted: 17 October 2022 Published: 26 October 2022 (* Corresponding Author)

Funding: This study received no specific financial support.

Competing Interests:The authors declare that they have no competing interests.

1. Introduction

Many research projects have studied the food industry in different countries. It is the largest industry sector within the European  Union  (EU) and most of the producers have  small companies (Hirsch & Gschwandtner, 2013). The sector is heterogeneous and it contains many segments. Consequently, food production companies run differently and deal with various   market forces.   Companies in the food retailing, dairy, restaurant and bakery industries may be differ from one another.  Despite the importance of bakeries to the economy, the bakery industry has only been the subject of a small number of published publications.  It may therefore be of great interest to take a closer look into this segment.

The market is quite similar across national borders, geographically well spread and employs many workers. Therefore, an analysis of Norwegian bakeries will be relevant to other countries and provide better insights into how the sector works. There are no advanced technologies associated with operating a bakery. It requires some investment but of limited scope. Therefore, a bakery is quite easy to establish.   Hence, there is considerable competition in this market. This probably sets limits on companies’ growth and on the achievement of high profits over a longer period. To find the long-run profit rate of bakeries of different sizes and ages, we use Mueller’s (1986) theory of profit persistency. It estimates the year-on-year relationship of profit rates which describes how long firms are predicted to stay above or below the sector’s average profitability. The measure can thus be interpreted as the importance of firm-specific factors as any differences in profitability are captured by the profit rate.

As Burroughs and Harper (2002) suggested that  bakeries can be divided into different segments. Bakeries are traditionally small local producers of baked foods; their size being restricted by the local demand. In the modern form of the sector, however, there are also bakeries that supply grocers or export their products.  Beyond fresh goods, such as bread and pastries, they also sell frozen and dried foods. Burroughs and Harper (2002) suggested that big companies are more profitable than smaller one because they have reached at the size at which scale benefits grow.  

There are not many obstacles to starting a new bakery, although becoming a large supplier or exporter of baked goods does involve several barriers. We investigate the profitability in this sector both between and within individual bakeries of different sizes.  This allows us to understand which bakeries are most profitable and when they are most profitable. Though the market in which bakeries operate well is  a perfect market, similar to that of the restaurants described by Opstad and Valenta (2022) the existence of large bakeries that supply grocers and export alters the state of the market.

This paper contributes insights into how markets with many small local producers and some large exporter’s function. The case of bakeries, traditionally producing key goods for society is interesting in and of itself but the lessons learned here have implications for other similar markets too. We find that bakeries must transition through a period of lower profitability to become large and highly profitable. We suspect that firms in other sectors might experience the same dynamic. This is important to know for those who run bakeries but also (potentially more importantly) for the financial institutions that provide loans to bakeries and other enterprises.

2. Profit Persistency (PoP) 

A central issue within microeconomics and market theory about companies is that the better the classic market economy works, the harder it is to achieve high profit rates over a long period of time. The profit rate deviation and its autoregressive process as presented by Mueller (1986) can be expressed as follows:

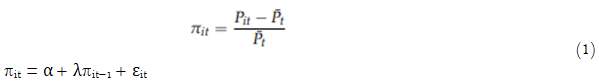
where   is the profit of company i at time t.measures the average profit rate for the sector in year t. Hence, πit will be firm i’s deviation from the average profit rate of the industry at time t. Equation 1 allows us to estimate the degree of profit persistence (λ) with dynamic panel data methods. The error term εit will have feedback bias if we estimate the equation with Ordinary Least Squares (OLS) which is why we use the system-GMM estimator developed by Arelleno and Bover (1995) and Blundell and Bond (1998). It is explained further by Valenta, Idsø and Opstad (2021).

The autoregressive parameter λ describes the correlation between last year’s profit rate (deviation) and this year’s profit rate for each firm. If a firm experiences a shock to its profitability causing it to be profitable than the sector mean, λ will measure the speed at which the profit rate adjusts to the sector mean profit rate. The autoregressive parameter can be interpreted as showing how successful firms are in keeping their profits high or how much they struggle to increase their profitability to reach the sector mean. The persistence of the profit rate (deviations) is thus understood as the stickiness of differences in profit rates across firms which is why the estimate can be interpreted as the importance of firm-specific factors. If the profitability of a firm does not predict its profitability the next year at all, the autoregressive parameter is equal to zero. If the past profitability completely predicts the future profitability, λ is equal to unity. The procedure is explained in more detail in Opstad, Idsø and Valenta (2021). The long-run steady-state equilibrium of the profit rate is defined as:

For companies to survive in the long term, their value  must be positive. A negative long-run equilibrium indicates that firms will have deficits in the long run. These firms will not survive and must cease operations. In this article, we focus on different segments of the bakery sector, that is, different types of bakeries varying specifically in their size and age. For instance, we are interested in determining the long-run profitability or equilibrium of new or large bakeries and making a comparison.

3. Literature Review

Short-run profit persistence seems to be lower for the food industry than for the rest of the economy. Using data from England and Italy, Goddard, Tavakoli and Wilson (2005) suggested a value  between 0.3 and 0.45 for the whole industry. Hirsch and Gschwandtner (2013) estimated λ for the food industry in the EU to be between 0.1 and 0.3 using GMM estimators. It should be noted that there is a substantial difference in the values across the EU countries. The estimated value for Belgium and Italy is between 0.1 and 0.15 that for France and Spain is between 0.2 and 0.25 and the highest value is for England with λ equal to 0.3. They explained the low persistency of profits for the food industry with strong price competition and limited dynamic growth with a few new products. In close to perfect markets, profits are competed away, leading to low persistency in profits. Kozlenko (2015) divided the food sector into subgroups. One of these was the manufacturing of baked goods. Unlike other parts of the food industry, he estimated λ to be equal to zero for the producers of baked goods; that is, there is no degree of profit persistence in this part of food industry.

Hirsch, Lanter and Finger (2021) studied food retail in three countries (Sweden, Spain and France). They found that large firms have considerable and persistent profit rates with values between 0.78 and 0.99. The variation of past profitability between firms explains between 78 percent and 99 percent of the variation in future profitability. For comparison, they found that the persistency of profit rates is about 0.3 or 30 percent for small firms. Parts of the food industry are dominated by major chains. These companies have considerable bargaining power with suppliers and major competitive advantages. These firm-specific factors lead to persistently high profits explaining the high values of the autoregressive parameter. 

Coad, Segarra and Teruel (2013) argued that learning and inertia effects might favour older firms. For two of the countries (Belgium and France), however, there was a negative relationship  between age and profit persistency. Majumdar (1997) justified this by arguing that old companies have become more bureaucratic and less efficient over the years. It may be the case that the differences in firm-specific factors are more drastic within young firms while these differences flatten as firms age. Pervan, Pervan and Ćurak (2017) confirmed a negative relationship between age and food industry profitability by using Croatian data. The reason might be that older firms are less flexible and less able to make changes that increase efficiency.

Goddard et al. (2005) found evidence for diseconomies of scale for large firms. This might not be the case for the food industry. Hirsch and Gschwandtner (2013) identified a positive correlation between profit persistence and size for the food sector in France, Spain and England. Pervan et al. (2017) confirmed a significant positive relationship  between size and profitability for the food industry. Kozlenko (2015) studied specifically producers of baked foods, finding a negative relationship between profit persistence and the size of the companies.   With regard to the relationship between size and profitability, reading literature revealed contradictory results with some studies reporting that small bakeries are the most successful   while others claiming that large bakeries are the most profitable. Hirsch et al. (2021) suggested a U-shaped association between profitability and size, with medium- sized producers being less successful than small and large ones.    This conclusion can be expanded upon in this article by considering micro bakeries. Newly established businesses confront several difficulties including inefficiency.  Inefficiency plays  a major role  in  firms declaring  bankruptcy. Deeds and Rothaermel (2003) showed that firms that survive will gradually learn to become more efficient.  According to an  article by  Opstad and Valenta (2022),  learning reduces one’s chances of going bankrupt.

Since there is great competition between bakeries and profits are low, a critical factor in survival is making a profit. Therefore, it is important to be effective (De Monte, 2020).   Good management and cost control are deciding factors (Hua & Templeton, 2010) while a major  cost component is the purchase of raw materials (Dyntar & Strachotová, 2018). For bakeries, good logistics and prevention of wasted raw materials are essential for turning a profit both for small and large producers.

It is difficult to survive in the sector  when times are tough , whether the demand or the supply is  constrains ,  many companies must leave the market (Carree & Dejardin, 2007). When the average profitability increases in the sector, more firms are attracted to enter it Opstad and Valenta (2022). This entry occurs with a time lag as entrepreneurs must complete a process to open a business. The bankruptcy related to decreases in the sector’s profitability is contemporaneous. Lastly, there is a positive relationship between growth and the number of entries in the market (Kaya & Ucdogruk, 2002). 

4. Hypotheses

The literature on microeconomic theory, economies of scale and the importance of firm-specific factors in terms of profitability bring up central ideas in economics. In this article, we use these fields to produce three hypotheses, which can be tested with our data from Norwegian bakeries from 2006 to 2019. The first hypothesis stems from the literature based on the seminal work of Mueller (1986).

Hypothesis 1: The largest restaurants in Norway have persistently high profit rates while the probability is high for new restaurants to face bankruptcy. We hypothesize that both large bakeries and new bakeries have the same characteristics.

Economies of scale are frequently discussed in the economic literature. Economies of scale can be achieved by countries and firms.   Hypothesis 1 raises the issue and hypothesis 2 explores it further by examining if scale is related to profitability in a non-linear way.   Other authors (Hirsch et al., 2021) have suggested that the relationship is U-shaped, with small and large food producers being more profitable than medium-sized producers. Burroughs and Harper (2002) suggested that large suppliers and exporters of baked foods are very profitable but small, local, family-type bakeries are also profitable compared with the sector average.  This potential non-linearity is examined by Hypothesis 2.

Hypothesis 2; Large bakeries are more profitable than smaller ones. Micro bakeries become increasingly profitable as they approach the minimum efficient scale. Beyond the MES, profitability is independent of size. The very largest bakeries function as distributers of baked goods and are the most profitable.

Firms entering markets in which the barriers to entry are low often enter with minimal investment. In other words, new firms are often small. These new firms are especially sensitive to market forces since they lack experience. If the average profitability of the sector declines, firms will  leave  the market in larger numbers than if the average profitability does not decline (Opstad & Valenta, 2022). This outflow of firms from the market happens contemporaneously and we believe that bakeries are no different.

Hypotheses 3: The outflow of bakeries, especially new bakeries are larger in years in which the average sector rate of profitability declines. The three hypotheses contribute significantly to the literature on profitability and scale in food producers ranging from large suppliers and exporters to local family-owned bakeries and from generations- old bakeries to newly opened bakeries.

5. The Data

From the Norwegian public register, we obtained the financial statements for about 700 bakeries in the period 2006–2019 (see Table 1). The data was  compiled by Wahlstrm (2022) described it thoroughly. Importantly, the Norwegian public register contains coding denoting the sectors within industries, making this analysis possible. Many authors on the European continent such as Hirsch and Gschwandtner (2013) have struggled to obtain such information. In addition to having these details, our data set includes information on whether the firms filed for bankruptcy in those years.

The variables that we investigated for the Norwegian bakeries from 2006 to 2019 in which all “rates” are defined as variable x divided by revenue, are the market share, the rate of profit, the rate of growth, the rate of debt, the rate of cost and the years in business. Table 1 separates the sector into six segments: bakeries that have been in the market since 2006 (established bakeries), bakeries that have entered the market since 2006 and stayed in the market (successful entries), bakeries that have filed for bankruptcy during the period (facing bankruptcy), large bakeries (those with more than   0.5 percent market share), micro bakeries (those with less than   0.05 percent market share) and small and medium-sized bakeries (those between micro and large bakeries).

For all the bakeries, the average rate of profit is just below 2 percent. The average rate of growth is above 6 percent, while the cost rate is 97 percent. Interestingly, the rate of indebtedness is very low for bakeries with the debt burden being less than half a year’s revenue. This is a characteristic of bakeries; the barriers to entry are low. Of the segments, the micro bakeries are the most indebted while the small and medium bakeries are slightly less indebted than the large ones. The bakeries facing bankruptcy, perhaps have the lowest level of indebtedness. The costs were higher than the revenues for the bankrupt bakeries, but their growth was only slightly lower than the growth for those who survived,

The rate of profitability is the highest for the largest bakeries and the oldest bakeries. There are many old bakeries that are large, and the average profit rate is about 5 percent. The firms that entered the sample during the sample year had no rate of profit while those that faced bankruptcy had substantial losses on average.

Descriptive Statistics	All Bakeries	Established Bakeries	Successful Entries	Facing Bankruptcy	Large Bakeries	SME Bakeries	Micro Bakeries
Market Share	0.21% (0.81%)	0.31% (1.07%)	0.09% (0.21%)	0.06% (0.07%)	1.56% (2.32%)	0.14% (0.08%)	0.02% (0.01%)
Profit Rate	1.78% (15.98%)	4.87% (16.56%)	0.14% (16.12%)	-3.53% (11.18%)	5.70% (12.75%)	1.41% (10.29%)	1.38% (19.85%)
Growth Rate	6.45% (21.48%)	2.56% (17.44%)	11.36% (23.53%)	10.94% (25.46%)	4.63% (9.14%)	4.63% (14.57%)	8.29% (27.03%)
Debt Rate	45.45% (44.62%)	47.09% (50.16%)	46.83% (41.44%)	36.37% (22.55%)	39.72% (25.26%)	36.65% (31.12%)	53.76% (54.30%)
Cost Rate	96.94% (16.78%)	94.56% (17.90%)	98.61% (16.27%)	102.51% (10.69%)	94.01% (12.14%)	97.38% (11.35%)	97.10% (20.78%)
Years in Business	13.95 (12.70)	19.71 (14.00)	5.96 (3.41)	8.79 (7.59)	26.11 (18.24)	16.64 (12.43)	9.53 (9.23)
Number of Entries	186	0	186	33	8	48	52
Number of Bankruptcies	89	0	0	89	0	37	130
Number of Bakeries	612	337	186	89	55	252	305

Note: Large bakeries are defined as having above a 0.5 per cent market share and micro bakeries as having below a 0.05 per cent market share, while small and medium-sized bakeries are in between.

 The core of the analysis in this article lies the rate of profitability. Table 1 presents the differences in the profit rate between the segments of the bakery sector. Table 2 shows the rate of profitability and the rate of growth within the sector throughout the sample years. The two measures do not seem to rise and decline together but vary to a degree. The rate of profit varies between 1.5 percent and 4.5 percent, while the rate of growth varies between 5.4 percent and 11.6 percent. We also detail the number of entrants and bankruptcies which are in the ranges of [8, 29] and [3, 17]. In the average year, about 300 bakeries operate which means that the entry and exit correspond to about 7 and 3 percent of the total population.

Descriptive	2006	2007	2008	2009	2010	2011	2012	2013	2014	2015	2016	2017	2018	2019
Profit Rate	2.6%	2.7%	1.5%	3.0%	1.6%	2.6%	1.6%	3.9%	4.0%	3.5%	2.3%	3.3%	2.0%	4.5%
Growth Rate	-	9.2%	6.3%	8.8%	5.4%	11.1%	9.2%	11.6%	6.2%	9.0%	11.1%	10.6%	5.4%	10.4%
Entries	13	18	13	8	12	19	26	25	25	29	29	16	29	13
Exits	10	16	9	6	9	5	10	4	11	11	17	10	12	3
Firms	278	273	260	259	249	255	267	275	304	320	328	327	340	319

6. Methodology

In this analysis, panel data is used over a period of 15 years. We use different estimators for   each of the hypotheses. The parameters of the equation describing Hypothesis 1 are estimated using the generalized method of moments (GMM). The system-GMM that we use ensures consistent and unbiased estimates by correcting for the potential feedback bias caused by correlated error terms. The feedback bias occurs since the error term is equal to this year’s value minus the value predicted by last year’s value. Since last year’s value is both an explanatory variable in this year’s equation and an endogenous variable in last year’s equation.  It must be the case that there is a correlation between the error term and the lagged dependent variable. That is, since Yit-1 creates Uit through the previous estimation of the AR parameter, then Yt-1 must be correlated to Uit. To solve the feed-back loop, instruments are usually used in a GMM framework. By using the difference between last year and the year before that to instrument for this year’s level, no bias should be expected. But since the correlation between last year’s growth and today’s level diminishes as the level approaches a random walk. To solve this, the system-GMM estimator uses double-sided instruments.    The level of last year contributing as instruments for today’s growth. Monte Carlo simulations have shown that though the Arellano-Bond (AB)-GMM estimator struggles with high persistency series, the system-GMM has no immediate troubles.

As discussed in the literature review, some studies have found a non-linear relationship between profit and size (Hirsch et al., 2021). Dewan and Neligh (2020) applied this method to estimate cost functions while others used it for estimating profit functions (Amato & Amato, 2004; Goddard, 1983). The relationship between firm size and profitability is industry specific. Amato and Amato (2004) used linear, quadratic and cubic models for size correlated with profitability in US retailing. The argument was that large retailers have market power, and this gives higher profits. Table 1 shows the same profitability pattern. Big bakeries that supply goods across a larger district tend to have significantly higher than average profits in the sector. We include a cubic term with linear and quadric terms since we assume there is a minimum efficiency scale.

Before we continue with the analysis of whether the size of a bakery affects its rate of profit non-linearly, we must introduce two concepts. First, assuming that the effect is non-linear, we must investigate the degree of non-linearity. If the non-linearity is of the second degree, the equation will be:

The predicted values from Equation 3 will have either a U-shape or an inverted U-shape. The U-shape occurs when  is negative and is positive. Hypothesis 2 suggests that this is the relationship between size and profitability. If the non-linearity has a U-shape, micro bakeries and large bakeries are more profitable while small and medium bakeries are less profitable. Equations 1 and 2 and the answer to hypothesis 1 should indicate the same conclusion as Equation 3. 

In regular OLS regressions, the analysis based on the equation above ends here. With panel data, we have both a cross-sectional and a time series dimension. Consequently, we can estimate the equation in two directions. Evidence in support of Hypothesis 2 is most often analysed between firms. Using the traditional random-effect estimator, one must assume that the omitted variables affecting the rate of profit are distributed normally.  These omitted variables can affect the rate of profit but they must be distributed randomly with regard to size. If these omitted variables do affect both profit and size, we might suffer from omitted variable bias. In the econometric literature (Verbeek, 2017) this issue is formulated as the error term  with two components. The first component, , is the classic an error term which is assumed to have mean zero and constant variance. We use robust standard errors to correct the standard errors regarding potential autocorrelation and heteroskedasticity in the error term. The first assumption means zero, holds by the assumption that any omitted variables are placed in the second component, . That is, all constant or firm-specific omitted variables are assumed to be randomly distributed across Norwegian bakeries. Equation 4 shows the error term equation:

The random-effect estimator assumes that and, if this holds, the estimation will not suffer from omitted variable bias. The unbiasedness of the random-effect estimator hinges on this assumption. The assumption is most likely not to hold but the estimated parameters tell us important facts about the sector. Though causation may not be extrapolated if the estimators are biased.  The correlation can still inform us about the structure of the baked goods sector.

To avoid the potential bias described above, we also estimate the equation by using the fixed-effect estimator. Rather than assuming that the firm-specific variables are not related to the size of bakeries, the Fixed Effects (FE) estimator performs a within transformation of the equation. This is equivalent as expressing the following Equation 5:

The FE estimator removes all constant factors from the estimation through a within-estimation. This involves subtracting the mean of each variable from each observation. Since constant factors do not vary over time, they are removed from the equation. Unobservable constant factors that affect the dependent variable are also removed. Since every mean is removed, the fixed correlation between the explanatory variables and the error term is also removed. The bars represent the average value of each variable, not y and x, for each firm. This individual intercept removes all the constant variables contained in  by removing the individual average rate of profit and average size from each of the individual firms. Thus, there are no constant omitted variables left, although there can still be varying omitted variables influencing the estimator, but these are not as plentiful as the controlled ones. We will return to this discussion when the estimates are obtained, and we can analyse the non-linearity of the economies of scale effect.

The omitted variables issue is important but the intuition behind the two estimators must be understand too. The random-effect estimator uses the cross-sectional dimension of each year while the fixed-effect estimator uses the time series dimension of each firm. It follows that the estimated parameters must be interpreted differently. The between or Random Effects (RE) estimate tells us the predicted effect of size between firms. The between parameter can be interpreted as follows: if firm A is X larger than firm B, then firm A is predicted to be  more profitable than firm B.  The within or FE estimate, however, tells us about the predicted effect within firms. The within parameter can thus be interpreted as follows: if firm A is X larger in Year T+N than it was in Year T, then firm A is predicted to be  more profitable than in Year T+N.

The difference in interpretation might seem large but it is only dependent on the within transformation of two variables: profit and size. If the assumption  holds true, the two estimators must be quantitatively identical. Thus, if there are inherent or constant advantages or disadvantages that cause restaurants to be smaller or larger which also affect the rate of profit.  They will result in a bias of the random-effect estimator. Logically, any difference in the two estimates can be traced to the effect of inherent differences. In the equation above, the between estimator can be used if the goal is to understand whether bakeries of different sizes have different levels of profitability. If the interest lies in understanding the causal effect of a firm increasing or decreasing in size on its profitability, the within estimator must be used. While the within or fixed-effect estimator controls for all constant variables, it does so at a price. That price is that only variations within each firm can be exploited. If firms do not vary much regarding either size or profit rates, the estimates may be lacking in precision.

Most previous literature has assumed that size has a U-shaped or inverted U-shaped effect on profitability. The quadratic term models allow for turning or stationary points in the economy of scale effect. Based on the previous literature, we expect that there are two turning points: the minimum efficient scale and the point at which large bakery advantages are attained. Between the two points, we expect the economies of scale effect to flatten or even decrease, like a saddle. Consequently, we develop a cubic model:

Estimates of the cubic model will produce horizontal S-shaped predicted values lying either on the front or on the back. Since the squared and cubed variables produce large numbers, we divide the estimates by 10 and 100, respectively.

7. Findings and Discussion

7.1. Profit Persistency and Long-Run Profitability (Hypothesis 1)

The degree of profit persistence is significantly positive for the bakery industry (Table 3). This confirms Hypothesis 1. The value varies slightly depending on the size and whether companies are staying in, entering or leaving the market (H2 is confirmed). The highest value is among the large bakeries. It is rare for an  estimate  λ to be over 0.60, especially in the food sector, with its low entry barriers and simple technology (Giotopoulos, 2014). There are many indications that the effect in the bakery industry is the same as that in retail trade (Hirsch et al., 2021). Large retailing companies have a substantially higher profit and degree of profit persistence than others. The big chains dominate the market and have bargaining power and access to effective distribution channels. Some of the same effects apply within the baked goods sector as well. Due to their position in the market, large firms earn more than others and manage to keep a high profit rate from one year to the next. For bakeries facing bankruptcy, a profitable year is predicted to be followed by a year of losses, but this effect is not significant. For young (less than 4 years) and micro bakeries, the values of λ are positive but not significant. For survivors, old bakeries (more than 4 years) and those of a small or medium size (SME), the values of profit persistence are between 0.2 and 0.3. The degree of profit persistence is generally around 0.25 for Norwegian bakeries in the period. This is in line with other research for the service sector (Giotopoulos, 2014; Opstad, Idsø & Valenta, 2022). 

Variables	All Bakeries	Surviving Bakeries	Bankrupt Bakeries	Large Bakeries	SME Bakeries	Micro Bakeries	Young1) Bakeries	Old2) Bakeries
Persistency of Profit Rates	0.249*** (0.086)	0.245*** (0.092)	-0.120 (0.315)	0.664*** (0.105)	0.303*** (0.093)	0.158 (0.113)	0.122 (0.096)	0.289** (0.112)
Constant	0.021*** (0.005)	0.011 (0.008)	-0.017* (0.009)	0.012* (0.007)	0.015*** (0.004)	0.027** (0.011)	0.011* (0.006)	0.025*** (0.007)
Long-Run Equilibrium	2.80% [1.9, 3.9]	1.46% [0.4, 2.9]	-1.52% [1.8, 0.1]	3.57% [1.1, 8.2]	2.15% [1.4, 3.1]	3.21% [1.7, 5.2]	1.25% [0.5, 2.2]	3.52% [2.2, 5.3]
Observations	3,766	769	294	530	2,016	1,220	1,261	2,505
Number of firms	587	174	82	54	250	283	390	339

Note: 1) Younger than 4 years; 2) older than 4 years. Robust standard errors in parentheses. One standard error confidence interval in brackets. *** p<0.01, ** p<0.05, * p<0.1.

The long-run equilibrium calculated for the coefficients and constants above presents a clear picture. The bakeries that have filed for bankruptcy have an expected negative profit in the long run and must leave the market. In general, young firms have the lowest long-run profitability whether they have filed for bankruptcy in the sample period or not. These young bakeries have about a 1 percent margin of profit. Older bakeries have much larger margins above 3 per cent. Large bakeries are the most profitable in the long run while micro bakeries follow them closely. Interestingly, small and medium bakeries are noticeably less profitable.

7.2. Non-Linear Effect of Size on Profit Rates (Hypothesis 2)

The estimates in Table 3 suggest that micro bakeries and large bakeries are equally profitable in the long run, while small and medium –sized bakeries earn much lower rates of profit. Consequently, we estimate Equations 3 and 6 which model second- and third-degree non-linearity. Since non-linear estimates can be hard to interpret, we provide the predicted values of each regression. The predicted values plot indicates a U-shaped and a horizontal S-shaped prediction, respectively. We estimate the equations both between and within bakeries. The equation is logarithmic, but the x-axis shows eight intervals of market share percentages. Each new interval constitutes a two-to-threefold increase in size. We present two curves in each figure with a green line representing zero profits (when the marginal revenue is equal to the marginal cost). The curves represent the economy of scale effect between (blue) and within (red) bakeries. To show the spread of predicted values for each size, we also include shades around the curves which show the accuracy of our prediction. As Table 4 and Figure 1 show, the economy of scale does not need to be equal between and within bakeries.

Quadratic Model	Between (Blue) Profit Rate	Within (Red) Profit Rate
Linear	0.034 (0.039)	0.109*** (0.054)
Quadratic	-0.001 (0.001)	-0.003* (0.002)
Constant	0.260 (0.302)	-0.877** (0.415)
Observations	3,766	3,766
Number of Firms	587	587

Note: *** 1 percent significance level, ** 5 percent significance level, * 10 percent significance level.

The blue curve above reiterates the result found in the comparison of segments in Table 3.  The largest bakeries are the most profitable followed by micro bakeries while small and medium bakeries are the least profitable. The estimates closely mirror the results from Table 3, with predicted values ranging from 0 to 5 percent. Neither the linear nor the squared term is significant.  However, meaning that we cannot conclude that there is any economy of scale effect between bakeries. Within bakeries, the story is different. This method controls for all time-invariant or inherent variables that may cause both higher profitability and higher revenue. Importantly, decreases or increases along the x-axis must be interpreted as being within the individual bakery. The within estimation shows a very different situation from the long-run profitability in Table 3 and the between estimation. Both the linear and the quadratic terms are significant, and the predicted curve has an inverted U or bell shape. A bakery growing from being an average-sized micro bakery to becoming an average-sized SME bakery is predicted to have a large, 2–3 percentage point, increase in profitability. If an average SME bakery becomes an average large bakery, it is predicted to experience a substantial decrease in profitability of about 1–2 per cent.

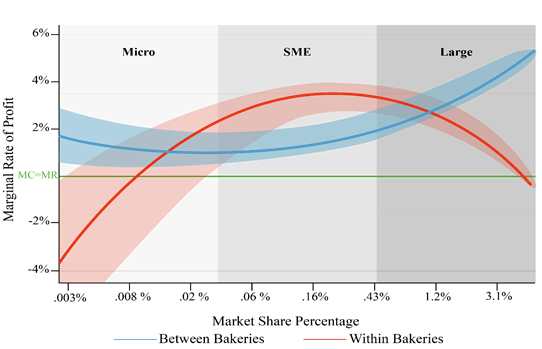
Figure 1. Quadratic economies of scale.

Though, these results are contrary to the claims in the previous parts of the article.  The reason is more obvious if we interpret them through the lens of shrinking bakeries. Bakeries facing bankruptcy often experience abrupt losses in their revenue and since the within estimator can only use variations within firms, these variations in profit and revenue might account for large portions of the total variation in the sample. The large variation of profitability in the very smallest bakeries also supports this claim: the within estimator predicts that an average-sized micro bakery will have a marginal rate of profit between 2 and -4 per cent. 

Cubic Model	Between (Blue) Profit Rate	Within (Red) Profit Rate
Linear	0.470 (0.158)	1.283*** (0.373)
Quadratic	-0.312* (0.189)	-0.791*** (0.239)
Cubical	0.069* (0.040)	0.162*** (0.051)
Constant	-2.325*** (0.230)	-6.867*** (1.929)
Observations	3,766	3,766
Number of Firms	587	587

Note: *** 1 percent significance level, * 10 percent significance level.

Turning to Table 5 and Figure 2, the cubic equation produces predicted profit rates with an even larger spread, especially within bakeries and for micro bakeries. When bakeries are very small, it is hard to predict their profitability.  The prediction lies in the range [-10, 5]. More importantly, unprofitable failing firms become very small, as seen in Table 4 and Figure 1. Within bakeries, the S-shape is clear. After the first stage of high instability in profit rates, the profit rate stabilizes. When it stabilizes, it begins to decrease slowly with an estimated percentage between the smallest and the largest SMEs. Larger bakeries are predicted to be much more profitable, the very largest enjoying a 10 per cent profit rate. The same is true between bakeries with the very largest bakeries being predicted to earn much more than the other segments.  Profitability seems to be stable for micro, small and medium-sized bakeries.

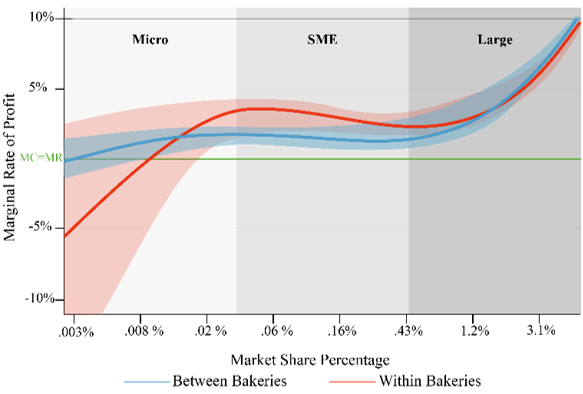
Figure 2. Cubic economies of scale.

The intermediate sizes exhibit profitability stagnation with respect to size both within and, to a lesser degree, between bakeries.  The profitability of small and medium sized bakeries seems to be declining as their numbers increase. There may be many reasons for this. Figure 3 zooms in on Figure 2, allowing us to see the dynamic more clearly at this intermediate stage. Figure 3 also includes a black line which is drawn between the average profitability of bakeries at each of the eight market share intervals. This black line shows a large drop in average profitability when bakeries have about a 0.02 percent market share. Neither method of estimation adequately captures this effect, but the actual interval averages do.

Firms must decide at some point in their growth whether to invest in growth or maintain their existing size.  firms’ size, At this point, new investments are made, mostly outside financing. The same might be true for bakeries, This explains why the predicted stagnation in profitability due to heavier debt burden will depress the marginal rates of profit. Many firms and bakeries might experience second large investment as a failure. However, the predicted values suggest some of those bakeries succeed and become large suppliers/exporters.

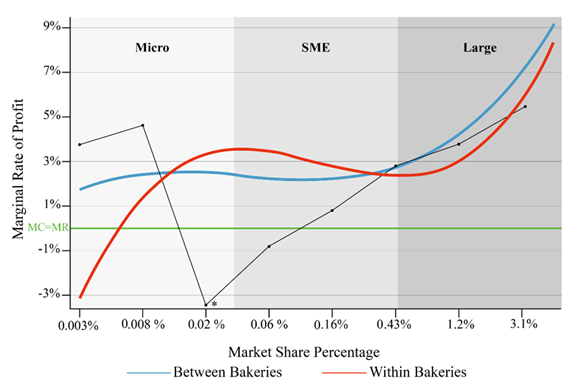
Figure 3. Economies of scale at the intermediate stage.

The above-mentioned findings and discussions are consistent with the previous literature on firm-level economies of scale. Many researchers have assumed that firms have an optimum size (Canback, Samouel & Price, 2006) but few have indicated that there are multiple optimum sizes. We demonstrated that there are several sizes for bakeries that can be considered optimal. There are some fixed costs associated with establishing a business (equipment, premises and more). As the production increases, the average cost decreases and economies of scale are achieved. We suggest that the optimum profitability is reached before this point as well occurring before local firms attempt expansion. In many cases, the production must exceed a minimum level to achieve a positive profit.  However, shown by the large variation in profitability attained by the very smallest firms. The higher the level of the minimum efficient scale is, the greater the barriers to entry are. This can make it difficult for newcomers to succeed. Some authors (Goddard et al., 2005) have argued that there are no longer any economies of scale. The advantages of scale have been exhausted, turning to diseconomies of scale. Increasing production beyond this point will reduce the profit rate. We find that this is true for the intermediate stage of bakeries, though we suggest that it applies to the average and not to all firms. The true relationship between size and profitability, however, is certain to vary from sector to sector.

Pervan and Mlikota (2013) reported a positive relationship between firms’ size and their profit rate in the food sector. We find a clear non-linear relationship. Just as in many other sectors, a certain level must be reached to have above average profits in the market for baked goods. Companies that have reached the MES level find that output beyond this will not reduce the profit rate. After some experience, companies learn how to secure profitable operations and fewer become bankrupt. In an interval of production beyond MES, there will be almost constant economies of scale. There is little impact from diseconomies of scale. The interesting point for the bakery sector is that the big companies have economies of scale. This finding is consistent  with the results of Burroughs and Harper (2002). There are obviously different segments within this sector. Large companies have more opportunities with marketing, manufacturing and deliveries over a larger geographical area. Many of them have a brand name that attracts more customers. We thus find many of the same tendencies for bakeries as Hirsch et al. (2021) described in retail trade.

7.3. Rate of Entries and Failures Depending on the Market Situation (Hypothesis 3)

There is little correlation between the profits and the number of entries in the same year (see Table 6). However, there is a strong and significant positive relationship to new businesses in the following year. We show this with correlation coefficients in the Table 6. The explanation is that it takes time to establish a business (gaining public approval, finding facilities, obtaining equipment, employees, financing, etc.). Therefore, there is a lag of at least 1 year. Based on economic theory, more entries will result in reduced profits. This may explain why there is a negative correlation between the number of firms coming to the market and the profit in the following year. The relationship between growth and entry and exit rates is as expected. Higher growth leads to fewer companies shutting down and more firms entering the sector (with a 1-year lag). The results confirm Hypothesis 3.

Most bakeries that file for bankruptcy are new businesses.  The average age of the bakery’s facing bankruptcy is 8 years, as shown in Table 1, but this average is skewed by some old bakeries that cease operations. In Figure 4, the distribution of age at bankruptcy is presented. To limit the x-axis, only firms under the age of 15 are included. Of the bakeries that filed for bankruptcy in this period, over 50 percent did so in their first 2 years in business. Within 5 years of business, 80 per cent of the bakeries that are now bankrupt filed for bankruptcy.

Aggregated Regressions	Profit Rate	Growth Rate
Growth (t)	0.43
No. of Exits (t)	-0.409	-0.221
No. of Entries (t)	-0.135	0.090
No. of Entries (t-1)	0.610	0.472
No. of Entries (t-2)	0.326	-0.093
Number of Firms	587	587

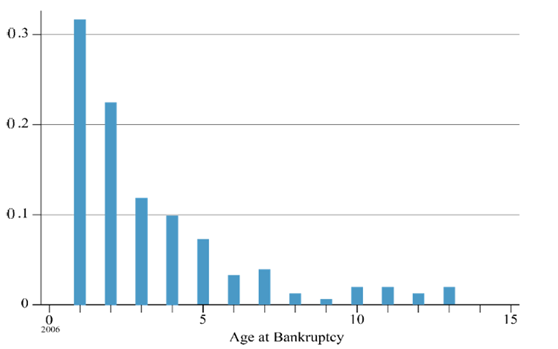
Figure 4. Distribution of age at bankruptcy.

The results for the Norwegian bakery industry are much in line with Opstad and Valenta’s (2022) findings for the Norwegian restaurant industry and confirm the basic classical market theories.  The rate of entries increases, and the rate of closures decreases when the industry is profitable. However, if more companies enter the sector, the profit rate will fall. Greater development facilitates entry and survival. Table 2 provides descriptive statistics for these topics. Table 6 presents the bivariate correlation coefficients between the variables.  There is a substantial negative relationship between failures and profit rates. The reason behind this statement is that, if the profitability in the sector decreases, fewer companies will decline.

8. Limitations

The current data is only delimited to one country. This limits our analysis, although there are many similarities in the way in which bakeries work in different countries. Since the analysis is based only on tax data.  We do not have data on the strategy of the various bakeries or the reasons why some enter, and others leave the market. Furthermore, we do not control for other continuous variables that may influence size or profitability in our analysis.

9. Conclusion

In this article, we presented three hypotheses. First, we find that large bakeries have persistently high rates of profitability. We also discover that, though new bakeries have marginal rates of profit, they are more likely to survive than to file for bankruptcy. The bakeries that do file for bankruptcy are new and the number that file for bankruptcy increases in the years when profitability is low in the sector. Despite financial growth the sector has experienced considerable growth since 2006. When the average sector profit increases, the number of bakeries entering the market also increases, although only after a year or two, as it takes time to establish a business.

The major contribution of this paper is the non-linear economies of scale effects that we identify in bakeries. We find that there are two distinct optimal sizes for bakeries: being a small local bakery and being a large supplier and exporter of baked goods. The first optimal point is related to the minimum efficient scale, describing the minimal scale of production that is needed to attain a stable and substantial flow of income.  Despite being small, these bakeries have a local and loyal customer.  The competition that they face need not be fierce, but they are at risk of large competitors entering their local market.

Bakeries that grow beyond this stage of the minimum efficient scale become an intermediate size which we predict to be characterized by stagnating or declining profitability. This stagnation and slight decline may be associated with the debt burden incurred to expand beyond the local scene.  Due to the low entry barriers for bakeries, the entrepreneurs in this sector may be lack the same level of experience as those in other sectors. This could be the reason for this second investment for further expansion, representing challenging times for these medium-sized bakeries.

The bakeries that prove to be successful in expansion proceed to the last stage of becoming a large supplier and exporter of baked goods. They become big national and potentially international players. These bakeries have attained substantial purchasing power, are clever in marketing and have a good system of distribution. They make deals with grocers, placing their products in stores across the country and within reach of a larger base of customers. These large producers of baked goods enjoy high profits and can keep their profits for long periods of time. 
The future will be interesting to behold since these large bakeries reach a large and wide customer base sustaining persistently higher rates of profits, which they can reinvest and grow further.  Bakeries may face the same situation as other sectors of the food and retail industry, with the market moving towards a concentration of large players dominating the sector. In this case, the profitable micro bakeries that we find in this study of Norwegian bakeries could be a thing of the past.

References

Amato, L. H., & Amato, C. H. (2004). Firm size, strategic advantage, and profit rates in US retailing. Journal of Retailing and Consumer Services, 11(3), 181-193.Available at: https://doi.org/10.1016/s0969-6989(03)00036-5.

Arelleno, M., & Bover, O. (1995). Another Look at instrumental variable estimation of error component models. Journal of Econometrics, 68(1), 29-51.Available at: https://doi.org/10.1016/0304-4076(94)01642-d.

Blundell, R., & Bond, S. (1998). Initial conditions and moment restrictions in dynamic panel data models. Journal of Econometrics, 87(1), 115-143.Available at: https://doi.org/10.1016/S0304-4076(98)00009-8.

Burroughs, R., & Harper, D. (2002). An analysis of profits within the Canadian food processing sector. No. 1391-2016-117050.

Canback, S., Samouel, P., & Price, D. (2006). Do diseconomies of scale impact firm size and performance? A theoretical and empirical overview. ICFAI Journal of Managerial Economics, 4(1), 27-70.

Carree, M., & Dejardin, M. (2007). Entry thresholds and actual entry and exit in local markets. Small Business Economics, 29(1-2), 203-212.Available at: https://doi.org/10.1007/s11187-006-6860-9.

Coad, A., Segarra, A., & Teruel, M. (2013). Like milk or wine: Does firm performance improve with age? Structural Change and Economic Dynamics, 24, 173-189.Available at: https://doi.org/10.1016/j.strueco.2012.07.002.

De Monte, E. (2020). Entry, exit and productivity: Evidence from French manufacturing firms. Working Paper. University of Strasbourgh.

Deeds, D. L., & Rothaermel, F. T. (2003). Honeymoons and liabilities: The relationship between age and performance in research and development alliances. Journal of Product Innovation Management, 20(6), 468-484.Available at: https://doi.org/10.1111/1540-5885.00043.

Dewan, A., & Neligh, N. (2020). Estimating information cost functions in models of rational inattention. Journal of Economic Theory, 187, 105011.Available at: https://doi.org/10.1016/j.jet.2020.105011.

Dyntar, J., & Strachotová, D. (2018). Does the pressure on increasing wages threaten the profitability of Czech bakery? ACC Journal, 24(2), 32–39.Available at: https://doi.org/10.15240/tul/004/2018-2-003.

Giotopoulos, I. (2014). Dynamics of firm profitability and growth: Do knowledge-intensive (business) services persistently outperform? International Journal of the Economics of Business, 21(3), 291-319.Available at: https://doi.org/10.1080/13571516.2014.921364.

Goddard, J., Tavakoli, M., & Wilson, J. O. (2005). Determinants of profitability in European manufacturing and services: Evidence from a dynamic panel model. Applied Financial Economics, 15(18), 1269-1282.Available at: https://doi.org/10.1080/09603100500387139.

Goddard, M. (1983). Selection indices for non-linear profit functions. Theoretical and Applied Genetics, 64(4), 339-344.Available at: https://doi.org/10.1007/bf00274177.

Hirsch, S., Lanter, D., & Finger, R. (2021). Profitability and profit persistence in EU food retailing: Differences between top competitors and fringe firms. Agribusiness, 37(2), 235-263.Available at: https://doi.org/10.1002/agr.21654.

Hirsch, S., & Gschwandtner, A. (2013). Profit persistence in the food industry: Evidence from five European countries. European Review of Agricultural Economics, 40(5), 741-759.Available at: https://doi.org/10.1093/erae/jbt007.

Hua, N., & Templeton, A. (2010). Forces driving the growth of the restaurant industry in the USA. International Journal of Contemporary Hospitality Management, 22(1), 56-68.Available at: https://doi.org/10.1108/09596111011013471.

Kaya, S., & Ucdogruk, Y. (2002). The dynamics of entry and exit in Turkish manufacturing industry. Middle East Technical University, Ankara, ERC Working Papers in Economics, 02/02,2002.

Kozlenko, I. (2015). Analysis of profit persistence in the Spanish food industry. Master Dissertation, Polytechnic University of Catalonia, Barcelona, Spain.  

Majumdar, S. K. (1997). The impact of size and age on firm-level performance: Some evidence from India. Review of Industrial Organization, 12(2), 231-241.

Mueller, D. C. (1986). Profits in the long run. Cambridge, UK: Cambridge University Press.

Opstad, L., Idsø, J., & Valenta, R. (2021). The degree of profit persistence in the tourism industry: The case of Norwegian campsites. International Journal of Economics & Business Administration, 9(4), 140–155.Available at: https://doi.org/10.35808/ijeba/739.

Opstad, L., & Valenta, R. (2022). The long-run equilibrium of industry population and bottom lines: Analysing the near-perfect restaurant industry. Journal of Applied Business and Economics, 24(3), 195.

Opstad, L., Idsø, J., & Valenta, R. (2022). The dynamics of the profitability and growth of restaurants; The case of Norway. Economies, 10(2), 1-12.Available at: https://doi.org/10.3390/economies10020053.

Pervan, M., & Mlikota, M. (2013). What determines the profitability of companies: Case of Croatian food and beverage industry. Economic Research, 26(1), 277-286.Available at: https://doi.org/10.1080/1331677X.2013.11517602.

Pervan, M., Pervan, I., & Ćurak, M. (2017). The influence of age on firm performance: Evidence from the Croatian food industry. Journal of Eastern Europe Research in Business and Economics, 2017(1), 1-10.

Valenta, R., Idsø, J., & Opstad, L. (2021). Evidence of a threshold size for Norwegian campsites and its dynamic growth process implications – Does Gibrat’s law hold? Economies, 9(4), 175.Available at: https://doi.org/10.3390/economies9040175.

Verbeek, M. (2017). A guide to modern econometrics (5th ed.). Hoboken, New York: John Wiley and Sons.

Wahlstrøm, R. R. (2022). Financial statements of companies in Norway. arXiv:2203.12842.Available at: https://doi.org/10.48550/arXiv.2203.12842.